Absolute quantification in the Droplet Digital PCR (ddPCR™) System relies on two elements: positive and negative fluorescence data from the sample droplets and data fitting to a Poisson distribution. After PCR amplification, the PCR-positive and PCR-negative droplets are individually counted on the droplet reader by passing them in a single stream through a fluorescence detector in a manner similar to flow cytometry. The number of target molecules initially present can be determined from the numbers of positive and negative droplets after amplification by probability analysis. Introduced in 1837, the Poisson distribution is a function that relates the probability of a given number of events occurring independently in a given sample when the average rate of occurrence is known. This section describes how ddPCR fluorescence data are obtained and how they are analyzed using Poisson distribution analysis in a ddPCR assay.
Related topics: Droplet Digital™ PCR (ddPCR™) Technology, Planning Droplet Digital PCR Experiments.
Page Contents
In the Droplet Digital PCR System, targets are amplified and detected using fluorescence-based probes. Positive (1) droplets, which contain at least one copy of the target, exhibit increased fluorescence over negative (0) droplets. In the ddPCR System, the QuantaSoft™ Software determines the numbers of droplets that are positive and negative for each fluorophore (for example, FAM and HEX or VIC) in each sample. The fraction of positive droplets is then fitted to a Poisson distribution to determine the absolute starting copy number in units of copies/µl input sample.
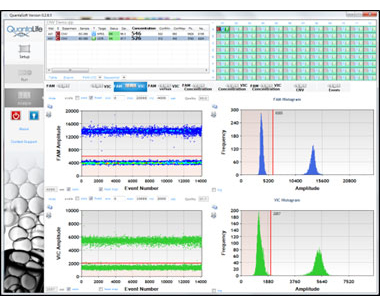
QuantaSoft data. FAM fluorescence is shown in blue, and VIC fluorescence is shown in green. The software counts the number of events (occurrences of each amplitude). In the plots at left, positive events are the data points in the upper range of the plot, and negative events are those below the pink baseline markers. QuantaSoft then plots the frequency vs. amplitude in the plots at right.
During droplet generation, template molecules are distributed randomly into droplets. Some droplets contain no template, some contain one template molecule, and others contain more than one. Due to the random nature of the partitioning, the fluorescence data after amplification are well fit by a Poisson distribution.
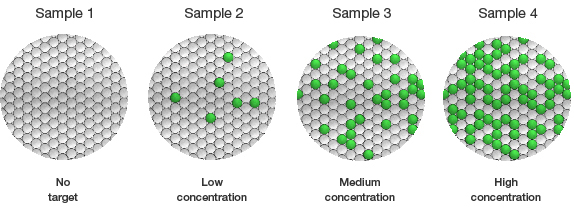
The number of positive droplets corresponds to the concentration of target in the sample.
According to Poisson’s law of small numbers, if there is a random distribution of quantifiable, independent events, predictions can be made about the likelihood with which these events occur. Thus, a Poisson distribution can be used to determine the number of template molecules in a droplet — how likely it is that 0, 1, 2, 3, or more template molecules are present in each droplet given the fluorescence data.
The plot below illustrates how a Poisson distribution is used to model the data from a ddPCR experiment. The value of ln(1-p), where p is the fraction of positive droplets, determines the number of target copies per droplet and thus the number of copies of target molecules in a 20 µl sample. These plots correspond to the 95% confidence level. The Poisson distribution can be used in place of other standard curves to determine template concentration, which means that data can be reliably obtained from the same samples across multiple instruments and laboratories.
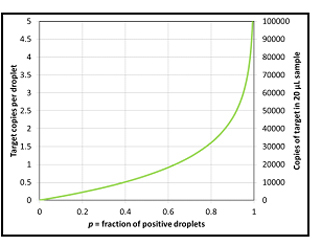
Application of a Poisson distribution to ddPCR data. Curve representing the relationships among the fraction of positive droplets, the number of target copies per droplet, and the number of copies of target in a 20 µl sample.
A common misconception about digital PCR is that for the technique to work properly, each partition must contain a single template molecule or no template molecules. In fact, the ddPCR System can reliably analyze samples containing multiple target copies per droplet. The Poisson distribution and fitting algorithm take variable numbers of template molecules into account to yield highly accurate concentration calculations.
The key to accurate Poisson analysis lies in optimizing the ratio of the number of positive events (positive droplets) to the total number of independent events (the total number of droplets). A greater total number of droplets results in higher accuracy for Poisson-based counting. With 20,000 droplets, the ddPCR System yields accurate starting template estimation from very low target copy levels to substantially high copy levels, providing a linear dynamic range of detection from 1–100,000 target copies. Estimation error is negligible compared with other error sources such as pipetting, sample processing, and biological variation.
Due to the statistical nature of this quantification method, the ddPCR System is most effective at low copy numbers; the major advantage of Droplet Digital PCR over real-time qPCR is the ability to resolve rare events and access targets at low template concentrations. For the analysis of very rare events, large samples can be divided into multiple 20 µl replicate samples to access a population of millions of droplets on a 96-well plate.

Quantification of template dilution. The results of a quantification experiment using a serial template dilution (A–E) are shown. Note that the relative numbers of negative and positive droplets in each dilution (the plots on the right) decrease as the sample becomes more concentrated; there are fewer negative droplets in samples at higher concentrations. Charts A–E represent data derived from each data point in the graph.
